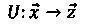Author: Tommi Kauppinen, tommi.kauppinen@helsinki.fi
Paulo Freire’s (1970) work on critical pedagogy has left us with far-reaching ideas of how critical approach to different aspects of the society can be helpful for people looking for change. Furthermore, Freire contributed to pedagogical discussion by showing schooling as a political institution. In addition, Freire shows clearly the dichotomy that exists in power relations. Freire himself called this dichotomy a relation between the oppressor and the oppressed.
One of the consequences of Freire’s work is discussion on critical mathematics (Frankenstein 1983, Skovsmose 1994, Valero 2004, Rawn & Skovsmose 2019), which demonstrates the possibilities of mathematics education to transform the society.
Addressing the critical role played by mathematics in society implies an understanding of the risks and uncertainties that mathematics and societal progress conveys. In the field of mathematics education, a critical approach can involve confronting students with situations in which mathematics seems to format the way they understand and act upon reality. (Pais et al. 2012, p. 1).
Pais et al. (2012) show the key element of critical mathematics: the way applied mathematics “formats” our understanding of the society. This blog post seeks to alleviate this formatting by showing how applied mathematics can be used in different ways to generate new possibilities for understanding societal interactions. Moreover, the discussion is held on possible new society-applied mathematics that would enable a way forward in the current stalemate of economic growth and environmental concerns.
Here society-applied mathematics and options to current mathematical concepts available are emphasised. The blog post considers first the present understanding of applied mathematics, shows how this can be transformed into a more sustainable view, and relates this discussion on individual gain. The developed concepts are then applied to environmental aspects of economics and utilized to develop novel mathematical conceptualisation, e.g. new formulations concerning of game theory and microeconomics. The idea of shared utility, where individuals benefit also from giving (e.g. Berking 1999) as well as getting, can then be directly applied to the concerns of anthropocene.
The reconceptualisation of some key elements of economics is not to undermine the use of the conservative economic calculus. The concepts introduced are backwards compatible with well-tested economic theory, but they show that there exists a wealth of alternative applied mathematics that is available to rethink societal interactions. Even without accepting the concepts in this blog post, one is confronted with the possible use of mathematics as a spearhead for a new framework in which societies can function. This notion relates directly to the foundation of critical mathematics (e.g. Kauppinen 2019, in Finnish).
Society-applied mathematics
Mathematics is the science of logical structures (e.g. Putnam 1967), and applied mathematics tries to employ these structures to identify them an empirical use. To find empirical uses for mathematics is not simple and some abstractions, approximations and assumptions are needed to mold the phenomenon under scrutiny into a meaningful equational form. This holds also for technical and business-oriented studies, but here the focus is on society-applied mathematics. One could define this type of mathematics as political mathematics, because there is a need to identify the ethical and political dimensions (Rawn and Skovsmose 2019) of society-applied mathematics.
Mathematics is used in the society to describe it’s functions, but it is also possible that the description begins to redefine the social context which was originally described. This is something society-applied mathematics needs to take into the account when being developed and ultimately, the discussion needs to be taken to the objectivity of mathematics (e.g. Weyl 2009). Is mathematics objective? Are society-applied mathematics also objective? Does a model become objective just by using mathematical formulation? What is objectivity, anyway?
Daston and Galison (2007) note that objectivity itself is a relatively new concept, which evolved in the middle of 19th century and has gradually developed into its present form (see also a blog on the subject and a summary on Daston’s and Galison’s work). Why is objectivity such a pursued target for economics and envinronmental sciences? Because objectivity historically also takes a stand on freedom, moral good and just society.
Instead of freedom of will, machines offered freedom from will—from willful interventions that had come to be seen as the most dangerous aspects of subjectivity (Daston and Galison 2007, p. 123) … It is this internal struggle to control the will that imparted to mechanical objectivity its high moral tone…(ibid. p. 178).
The notions of objectivity and justice relate to the present structures of the society, that are supported with mathematics. Moreover, the mathematics that is society-applied seldom has the reflective quality of redefinition when the needs of the society change. The demand for objectivity is here the key to understanding why this is so.
In addition, the mathematics does not often relate to demands of just society, but this is a crucial perspective into application of mathematics on a society level. When considering e.g. climate science, the mathematical models show climate as being a system in complex dynamic equilibrium, which can develop into many different climate states (e.g. Somerville 2012). It is therefore interesting to note that, firstly, mathematical modelling of climate reinstitutes climate as a system and, secondly, that it not only describes us the system but shows possible future scenarios. Both notions serve as examples of society-applied mathematics’ influence.
This discussion relates to critical mathematics, which can be put into two bullet points. The project of critical mathematics is two-fold:
Critical mathematics seeks to show that applied mathematics is always imperfect in relation to the issues in a real-world scenario (Frankenstein 1983), and
Critical mathematics tries to develop optional (albeit imperfect) solutions to technical, commercial and societal issues (Skovsmose 1994).
It is therefore the aim in this blog post, where some optional mathematics is developed for game theory and microeconomics, to find out novel ways of considering individual and shared utility.
Game theory and individual utility
Game theory offers a formal model for social interaction, which is often used in economic computation. In game theory, there is a predefined notion of each individual or group trying to maximise their own utility. Therefore, when game theory is used to characterize a negotiation, e.g. a climate negotiation, each party maximises their own utility and not the shared utility. In this section, the assumption of individual utility is eased and a novel solution to the classical prisoner’s dilemma is presented. This solution differs clearly from the traditional game theoretical solution to shared utility, namely cooperative games (Peleg and Sudhölter 2007).
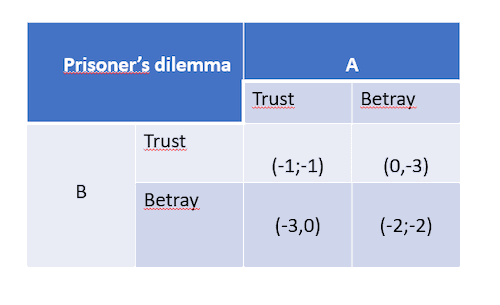
Prisoner’s dilemma (see Tucker & Kuhn 1950) defines a following problem: there are two individuals A and B, which are being accused of a crime they have committed and are being questioned. They can either (1) trust the other accused, or (2) betray the other accused. If they both betray one another, they both are imprisoned for two years. If both trust each other, both get one year of jail. If only one of them betrays the other, and the other one trusts, the one who betrayed gets free and the one who trusted gets three years of prison. In game theory, the situation can be described as in Figure 1.
Figure 1. Prisoner’s dilemma.
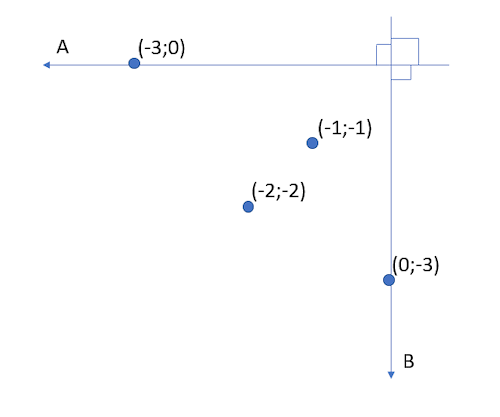
It is acknowledged that if both accused behave rationally, they are to give each other in. This is because the option to betray gives better results for the decision-maker, no matter what the other decides. If A is the decision-maker, then he gets free by betraying if B trusts (if A trusts, he gets a year of jailtime). If on the other hand, B betrays, then A only gets two years (if A trusts, he gets three years). In game theory, it is formally said that the decision to betray therefore dominates the decision to trust. In the following, we ease the assumption of individual utility to enable shared utility. First, the information in Figure 1 can be shown in two-dimensional plane just by plotting the numbered pairs (see Figure 2).
Figure 2. Prisoner’s dilemma in two-dimensional (A, B) coordinate system.
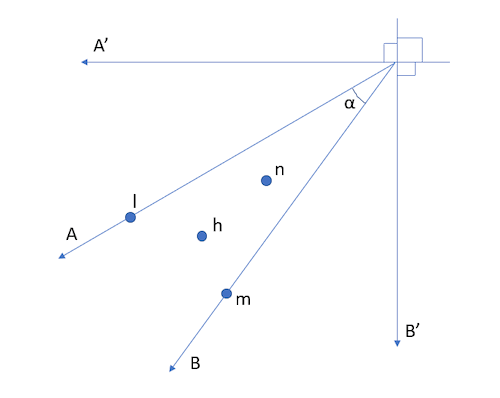
In the Figure 2, there is a right angle between the utilities of prisoners A and B. If the notion of individual utility is eased towards shared utility, the right angle is no longer necessary. In this case, the prisoner A gets part of the utility of prisoner B, and B gets some of the utility of prisoner A. Therefore, it is possible to release the right angle into an angle α (see Figure 3).
Figure 3. Prisoner’s dilemma in two-dimensional (A’, B’) coordinate system.
In Figure 3, the coordinate system is A’B’-coordinates, for when α is not a right angle, A and B do no longer trigger a two-dimensional coordinate system. However, the effect of the decision (trust/betray) can still be mapped on the Axes A and B, and the values can then be given in A’B’-coordinates.
Figure 4. Prisoner’s dilemma after coordinate system change, α = 36° = π/5 rad.
In Figure 4, the results for prisoners A and B are given, when α = 36°. Numerically it seems that the situation has reversed. Before (see Figure 1) it seemed that both prisoners A and B should betray one another (betrayal dominates trust), now it seems (Figure 4) that they should trust each other (trust dominates betrayal). What has changed?
It is paramount to note that in the solution presented the premises of game theory have been modified. When right angle between the individual utilities of prisoners A and B is released into angle α, at the same time the notion of shared utility is presented: part of the well-being of prisoner A comes from the well-being of prisoner B and vice versa. Next, the notion of shared utility is formalised using utility series.
Shared utility as utility series
It is of interest to find a formulation for shared utility, as many societal issues stem from the fact that people are advised to maximise their individual utility. By finding a sound basis for shared utility, which was already used in game theoretical setting, one can hope to affect the discussion held in many forums on utility. This is clearly a project embarked on with the help of critical mathematics.
In economics, a utility is a mapping U, s. t.
where x is n-vector, which describes the resources needed to attain the utility z. Total utility id given by z, which is a m-vector, and both n and m belong to natural numbers. Therefore,
U(x) = z.
Let us assume we have a infinite series q1,q2,…,qi-1,qi,qi+1,…, and that the sum of this utility series is as follows:
In addition, assumption is made that 0 ≤ qi ≤ 1 with all i, qi≥qi+1 with all i, and that Q=1.
Now one can reframe the utility function given above with the multiplier Q (=1). One gets
U(x) = Qz.
The utility function given through the utility series is almost the same as the traditional utility function. However, one can now assume that the utility series Q includes preference relations qi, which describe the preferences of an individual as follows: q1 is the individuals own gain, q2 is the gain received by his most important thing or being, q3 the gain of the next important, and so on, as long as there are preference relations to identify and define. One may not that this classification is made on a cardinal scale, where the numerical values are defined only in relation to the other values given. As an example, qi can be given the following values: q1=0.5, q2=0.2, q3 = 0.2, q4=0.1, qi>4 = 0 satisfy the conditions given to the members qi of utility series above. We may also note that in a classical formulation, q1=1 and the rest qi, i ≠ 1, are zero.
To create a possibility to have different utilities, one needs to consider the utility z transforming with every different qi, in effect giving zi. It should be noted that now we differ from the classical formulation, but justifiably so, as the different types of utilities with preference relation qi need different numerical values. One gets
It is now evident that when utility function is calculated, there are shared utilities with other individuals. To account for these shared utilities, one considers the following in relation to given qi and zi pair:
Uown(x) = qizi, and
Ushared(x) = Aqizi.
The Uown gives individual’s own utility, but the Ushared is the benefit of the shared utility to the receiver of the utility, considering the resources x used by the giver of the utility. The alteration matrix A gives the mapping of the utility of the giving individual as utility of the receiving individual. In general case, then, A is a m x m matrix.
One more thing to consider is the total utility Utot of an individual. It is formulated by
Utot(x)= Ʃ Uown(x) + Ureceived,
where Ureceived = Ʃ (Ushared (by others with the individual)) is the amount of utility shared with the individual by others.
It is of interest to note that in this formulation, one unit of certain resources, e.g. money can amount to a total of more than one unit, which makes utility a more complex system than a zero-sum game.
As an example, let us consider monetary utility. Let us assume that there is a movie theatre, which shows a movie. Each film enthusiast gives ten euros to see the film and let us assume that 10,000 people do this. Let us consider these people as an average, having a utility function U(x) = Ʃ Uown(x) = -x1+ p x2, where x1 equals money spent on work-related expenses and x2 equals time individuals on average spend working and p is the average salary.
Let us assume that the film has utility series qi value of qi =1/256 for every individual and that the average salary is 2560 EUR. Then each of the ten thousand individuals has Ushared = A*10 EUR, and alteration matrix A is (m=1) a scalar with value of A=1. Therefore, the film makers (neglecting the movie theatre and other beneficiaries) receive a shared utility of Ureceived = 10,000*10 EUR = 100,000 EUR.
How can the game theoretical finding in the last section be formulated with utility series? This is clearly a case of relation between q1 and qi, as this relation determines the amount of shared utility between the prisoners. From the Figure 3 we can (when α = 36° = π/5 rad) solve (when we know that the angle is defined by (90° - α)/2):
qi/q1 = tan [(π/2 - π/5)/2 rad],
which gives
qi/q1 = 0.5095.
It is therefore appropriate to note that the relation between prisoner’s own utility and shared utility in the utility series must be little over a half to account for the emergence of trust in game theoretical setting.
Finding resource limits for sustainability
One can use the same mathematical structure as in the utility series to find for use of resources x in the utility functions. Now we can impose a limit on these resources x by calculating the total carbon budget for each individual (Le Quere et al. 2015) as approximately 0.7 tons of CO2-eq. per individual on this planet.
Let us then have all the resource vectors used in an ordered series s. t. x1,x2,…,xi-1,xi,xi+1,… scaled according to the total resource use possible. In effect, one gets
0 ≤ xi ≤ 1 with all i, xi≥xi+1 with all i, and that sum of these resource vectors is X=1.
It is therefore applicable to further limit the possible utilities by giving resource use limits as well. It can be noted that this limiting makes it more important to have shared utilities, as individuals can find it hard to fulfill their needs by just maximizing their own utility. Really, what ought to be done is to maximise own total utility by receiving as much shared utility as possible. It is left to the reader to imagine possible ways to do this, but examples are plenty. Rewarding social interaction can be one way forward.
Conclusion
This blog post demonstrates the power of critical mathematics both in finding novel ways of thinking but also in providing political alternatives to common societal issues. It is clear, that the models presented are introductory, and they need to be further refined to deal with exceptions. However, the whole process of understanding and evaluating these models is a process in critical mathematics and a possible learning process for all interested in mathematical thinking. One would hope that this learning process sparks more vivid and free relationship with mathematical creativity, not bounded by traditional right and wrong answers.
One can also note that shared utility therefore is a type of crossbreed between economic, environmental and social resource use. The exact modelling of these utilities is more involved than in classical models, but these pose no difficulty to modern-day computing power of e.g. a basic laptop.
There are infinite amount of mathematical structures and some of them can be applied to societies. There should be scientific discussion on the effects of using certain mathematical models on society-level, and political discussion on the alternatives available for current mathematics applied in the societies.
References
Berking, H. (1999). Sociology of giving. Sage.
Daston, L. & Galison, P. (2007). Objectivity. The MIT Press, US
Frankenstein, M. (1983). Critical mathematics education: an application of Paulo Freire's epistemology. The Journal of Education. 165 (4), 315–339.
Freire, P. (1970). Pedagogy of the Oppressed. (Pedagogia do oprimido). New York: Continuum, 2007.
Kauppinen, T. (2019). Oikeudenmukaisuus ja matematiikka – kohti soveltavan matematiikan poliittisuutta. Wordpress Blog. (in Finnish). URL: https://oikeudenmukaisuusjamatematiikka.home.blog
Le Quéré, C., Moriarty, R., Andrew, R. M., Peters, G. P., Ciais, P., Friedlingstein, P. & Boden, T. A. (2015). Global carbon budget 2014. Earth System Science Data, 7(1), 47-85.
Pais, A., Fernandes, E., Matos, J., & Alves, A. (2012). Recovering The Meaning Of "Critique" In Critical Mathematics Education. For the Learning of Mathematics, 32(1), 28-33.
Peleg, B., & Sudhölter, P. (2007). Introduction to the theory of cooperative games (Vol. 34). Springer Science & Business Media.
Putnam, H. (1967). Mathematics without foundations. The Journal of Philosophy, 5-22.
Ravn, O. & Skovsmose, O. (2019). Connecting Humans to Equations. Springer International Publishing.
Skovsmose, O. (1994). Towards a critical mathematics education. Educational Studies in Mathematics. 27 (1), 35–57
Somerville, R. C. (2012). Communicating the science of climate change.
Tucker, A., W. & Kuhn, H., W. (eds.) 1950. Contributions to the theory of games, Annals of Mathematical Studies.
Valero, P. (2004). Socio-political perspectives on mathematics education. In Researching the socio-political dimensions of mathematics education (pp. 5-23). Springer, Boston, MA.
Weyl, H. (2009). Philosophy of mathematics and natural science. Princeton University Press.